EmSAT Math Statistics Sample Questions with Answer explanation

Last updated on September 28th, 2022 at 04:23 pm

EmSAT Math Statistics Sample Questions

Question 1

Identify Statistical data type for the following variable: a medal won at the Olympics (Gold, Silver, Bronze, None)  

A) Nominal

B) Ordinal

C) Interval

D) Ration

Answer: A

Definitions:

• Nominal – applies to data that consists of names, labels, or categories

Example: John, Male, Female

• Ordinal – applies to data that can be arranged in order

Example: Happy, very happy, ok

• Interval – applies to data that can be arranged in order. The addition and differences between data values are meaningful

              Example: Temperature in Degree, SAT Score

• Ratio – applies to data that can be arranged in order. Ratios of data values are meaningful

              Example: Age, Height, Weight

May Be You Like: How To Prepare for EmSAT

Question 2

Here are the score of 20 students on an Algebra test. Find the mean of data set

Score	0	20	40	60	80	100
Frequency	3	1	2	4	8	2

Answer: 59

Mean (Average) = Sum of score numbers

                                  Total Number of student

                                = (0 x 3) + ( 20 x 1) + ( 40 x 2 ) + ( 60 x 4 ) + ( 80 x 8 ) + ( 100 x )  

                                                                                   20

                              = 1180

                                     20

                              = 59

EmSAT Math Statistics Sample Questions with the Answer explanation

https://youtu.be/pFuI-2s-4dc

Question 3

Ahmed and Hamad plays tennis each week. The probability that Ahmed wins the first match is  .

What is the probability that Ahmed wins exactly three of next four matches against Hamad.

A) 32/81

B) 32/243

C) 16/243

D) 8/81

Answer: A

This question is based on conditional probability. Conditional probability is represented by the formula

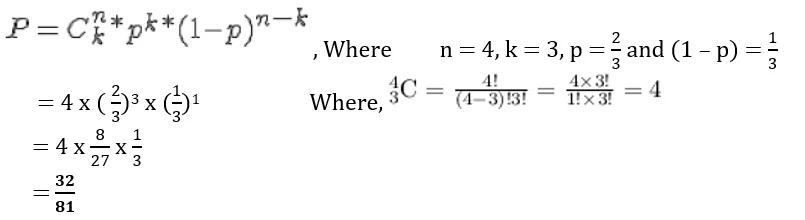
Question 4

The average rainfall for the years since 2005 is given below

Year	2005	2006	2007	2008
Amount in cm	1.345	1.408	1.537	1.580

In 2010 there was 2.956 cm of rainfall. How much more rain fell than predicted by the table above.  Round your answer to the nearest hundredth.

Answer: 1.28

 To find the predicted rainfall, find the differences between the each year of rain fall.

Average rainfall increased from 2005 to 2006 is 6.3% 

1.408 – 1.345 = 0.063 or 6.3% 

 Average rainfall increased from 2006 to 2007 is 12.9%

1.537 – 1.408 = 0.129 or 12.9%

Average rainfall increased from 2007 to 2008 is 4.3%

1.580 – 1.537 = 0.043 0r 4.3%

To find predicted rainfall for 2010, consider the middle value in percent change (i.e 6.3%)

1.580 + 0.063(1.580) = 1.6795

Therefore, predicted average rainfall in 2010 according to table is 1.6795

Find the difference between actual rainfall and predicted rainfall in 2010

2.956 – 1.6795 = 1.276

Rounding it to nearest hundred gives value of 1.28

Therefore 1.28 cm is more rainfall predicted by table

Question 5

The height of boys in a grade 10 class are normally distributed with a mean of 168 cm and standard deviation of 2.5 cm. In which range do 95% of the height approximately falls?

A) 160.5 – 168 cm

B) 160.5 – 170.5 cm

C) 163 – 173 cm

D) 163 – 175.5 cm

Answer:  C

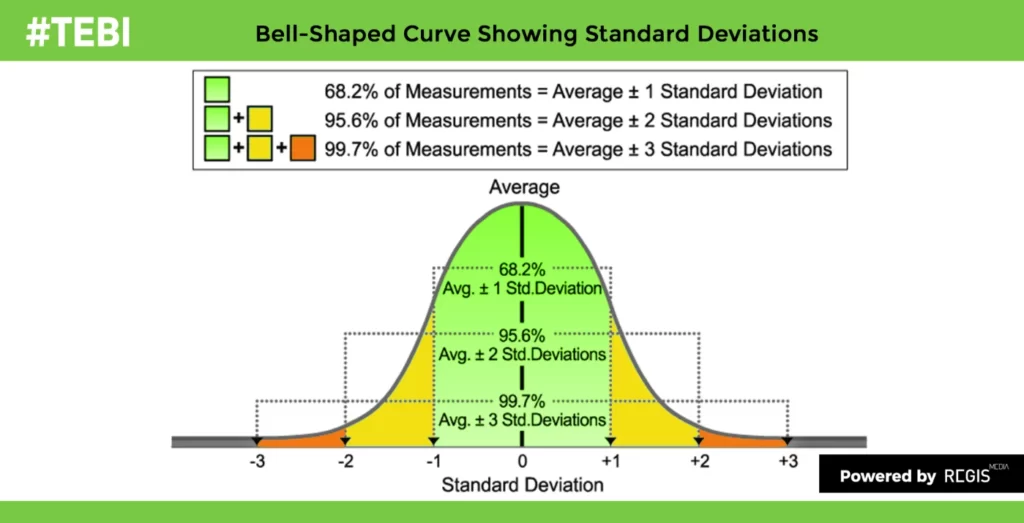
Range of height fall under 95% is given as

Range = Mean ± 2 (Standard Deviation)

Mean or average = 168 cm

Standerd deviation = 2.5 

Therefore, upper range = 168 cm+ 2(2.5)

                                              = 168 + 5

                                              = 173 cm

Therefore, lower range = 168 cm – 2(2.5)

                                              = 168 – 5

                                              = 163 cm

Range in between height falls 95% is 163 cm –  173 cm

Inquiry Now for Online / Offline EmSAT Coaching