40+ EmSAT Math Sample Questions with Answer Keys (2023 – 2024)

Last updated on May 14th, 2023 at 09:05 pm

EmSAT Math practice test helps students to understand the test structure and have real-time experience with the test. The test includes questions from most of the topics which are commonly tested on the actual EmSAT math exam.

Answer keys provided at the end of the test help you to do self-correction and plan your studies according to the topics which are difficult.

Proper Choice provides a complete preparation course for the EmSAT Math, if you need any help in preparing for the exam you can contact us for further details

This practice test includes 41 questions. You can keep a self-timer of 90 minutes and try to do the test in the specified time

1. What are three positive consecutive integers when product of the first and second is 2 more than 9 times the third?

A. 8, 9, 10

B. 9, 10, 11

C. 10, 11, 12

D. 11, 12, 13 

2. If 16 + 4x is 10 more than 14, what is the value of 8x?

A) 2

B) 6

C) 16

D) 80

3.  9 times the difference of 3a and b is

A. 9 x 3a – b

B. 9(3a – b)

\[C.\ \frac{3a-b}{9}\]

D. 27a – b

4. The expression below is undefined for which of the value(s) of x?

\[\frac{-11xy+15x^2}{x+3}\]

A. – 3

B. 0

C. 1

D. 3

5. h = – 4.9t² + 25t

The equation above expresses the approximate height h, in meters, of a ball t seconds after it is launched vertically upward from the ground with an initial velocity of 25 meters per second. After approximately how many seconds will the ball hit the ground?

A) 3.5

B) 4.0

C) 4.5

D) 5.0

6. Factor completely

9x⁵– 30x⁴ + 25x³

A.  9x²(3x + 25)

B.  9x³(x² – 21x + 16)

C.  x³(3x – 5)²

D.   4x²

7. The coordinate points (2, 5), (5, b), and (10, 34) are on the same line. What is the value of b?

A. 17

B. 18

C. 19

D. 20

8. Abdullah wants to be a part of school football team. The criteria for selection is that height (h) must be greater than 150 cm and no more than 180 cm. Which of the following inequality represents this relation?

A. 150 cm ≤ h < 180 cm

B. 150 cm ≤ h ≤ 180 cm

C. 150 cm < h < 180 cm

D. 150 cm < h ≤ 180 cm

9. 2x + 3 < – x + 9, what is possible value of x?

A.  – 2

B.     2 

C.     4

D.    6

10. In the system of equation below, if y >0, what is the solution to the equation?

   2x – y² = 3

– 3x + 2y² = –1 

\[A.\ \left(-5,\sqrt{7}\right)\]

\[B.\ \left(-5,-\sqrt{7}\right)\]

\[C.\ \left(5,-\sqrt{7}\right)\]

\[D.\ \left(5,\sqrt{7}\right)\]

11. In the system of linear equation below, what is the value of 3m + n?

5m – n = 11

2m – 2n = 9

A.  – 2

B.  0

C.  2

D.  4

\[12.\ The\ product\ of\ complex\ number\ -5+\sqrt{7i\ }and\ its\ conjugate\ is?\]

A. 32

B. – 32

C. 23

D. – 23 

13. Convert the complex number shown below to polar form

5 + 4i

A. 6.4(cos 38.65° + i sin 38.65°)

B. 6.4(sin 38.65° + i cos 38.65°)

C. 5(cos 40° + i sin 40°)

D. 5(sin 40° + i cos 40°)

14. Simplify: x³ • x^-7• x

A. x ^{– 3}

B. x¹¹

\[C.\ \frac{1}{x^{-3}}\]

\[D.\ \frac{1}{x^3}\]

\[15.\ Simplify\ the\ \exp ression\ \frac{27a^3}{b^5}x\ \frac{\left(9a^{-3}b^5\right)^{-1}}{a^5b^{-3}}\]

\[A.\ \frac{3a}{b^7}\]

\[B.\ \frac{243b^5}{a^5b^2}\]

\[C.\ \frac{3a^{-3}}{b^{-5}}\]

\[D.\ \frac{243a}{b^7}\]

16. Use the function f below to answer the question that follows.

f(x) = x² – 2x – 24

If f(x + 3) = x² + kx – 21, what is the value of k?  

A. 1

B. 2

C. 3

D. 4

17. If f(x) = 2x and g(x) = x³, what is (f o g)(-3) ?

A. – 6

B. – 27

C. 54

D. – 54

\[18.\ If\ f^{-1}\ \left(x\right)=\frac{5x-8}{3},\ which\ of\ the\ following\ is\ the\ function\ f\left(x\right)?\]

\[A.\ f\left(x\right)=\frac{3x+8}{5}\]

\[B.\ f\left(x\right)=\frac{8-3x}{5}\]

\[C.\ f\left(x\right)=\frac{5}{3x+8}\]

\[D.\ f\left(x\right)=\frac{5x-3}{8}\]

19. What is the domain for the function shown below?

f(x) = 2x² +  2

A. ( – ∞, ∞ )

B. (– ∞, 2]

 C. [– 2, ∞)

D. (– ∞, 2] u [ – 2, ∞)

20. Which of the following function is diversing?

\[A.\ f\left(x\right)=\frac{2x+10}{x^2}\]

B. f(x) = x² + 2

\[C.\ f\left(x\right)=\frac{3x+10}{x}\]

\[D.\ f\left(x\right)=\frac{4}{x^4}\]

21. Find the angle between vectors u and v (Round your answer to nearest integer)

U = 6i + 2j and V = – 4i + 3j

A. 124°

B. 125°

C. 126°

D. 127°

22. What is the tenth term of geometric sequence 4, – 12, 36, ……?

A. – 120

B. 236,196

C. – 78,732

D. – 59,045

\[23.\ if\ x=7,\ \log_2\ \left(x+2\right)\ +\log_2\ 3\ is\ equal\ to?\]

\[A.\ \log_2\ 12\]

\[B.\ \log_2\ 27\]

\[C.\ \log_2\ 30\]

\[D.\ \log_2\ 37\]

24. What is the value of x, if lnx + ln4 = ln8

A. 2

B. 3

C. 4

D. 5

25. An observer standing 50 meters away from a building notices a flagpole on the top of the building. If the angle of elevation to the base of the flagpole is 46.2º and the angle of elevation to the top of the flagpole is 50.1º, what is the height of the flagpole?

A. 2.3 m

B. 2.5 m

C. 59.8 m

D. 7.7 m

\[26.\ In\ a\ right\ triangle,one\ angle\ measures\ x°,\ where\sin x°=\frac{3}{5}\ What\ is\ \cos\left(\frac{\pi}{2}-x°\right)?\]

\[A.\ \frac{4}{5}\]

\[B.\ \frac{3}{4}\]

\[C.\ \frac{3}{5}\]

\[D.\ \frac{4}{3}\]

27. Angle C is a right angle in the triangle shown below.

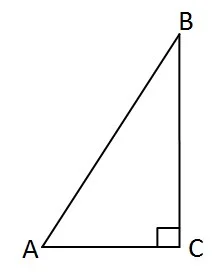
Which statement must be true?

A. Sin A = Tan B

B. Cos A = Sin B

C. Sin A = Sin B

D. Cos A = Tan B

28. Find the exact value of csc(- 420°)

\[A.\ -\frac{2\sqrt{3}}{3}\]

\[B.\ \frac{2\sqrt{3}}{3}\]

C. 2

D. -2

29.

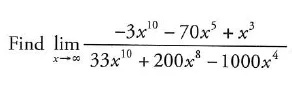
\[A.\ \frac{-1}{3}\]

\[B.\ \frac{-1}{11}\]

C. -3

\[D.\ \frac{-1}{33}\]

30. Which of the following statements is/are true about the function?

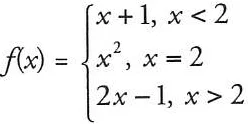
\[1.\ \frac{\lim}{x→2}\ f\left(x\right)\ exist\]

2. f(2) exist

3. f(x) is continuous at x = 2

A. 1 only

B. 1 and 2 only

C. 2 and 3 only

D. 2 only

31. The graph of the function f is shown below.

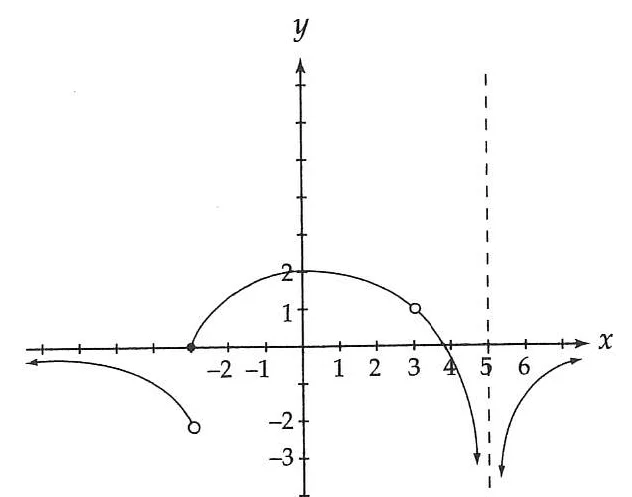
Identify the number of values of x in the open interval (- ∞, ∞) where f is discontinuous. 

A. One

B. Two

C. Three

D. Four

32. A circular pool of water is expanding at the rate of 16π in.²/sec. At what rate is the radius expanding when the radius is 4 inches?

A. 2

B. 4

C. 6

D. 8

33. If the position of a particle at time t is given by the equation x(t) = t³ – 11t² + 24t, find the acceleration of the particle at time t = 5. 

A. – 11

B. 0

C. 8

D. 11

34. Find the Derivative of ln(sin x).

A. Cos x

B. Sec x

C. Tan x

D. Cot x

35. Find the derivative of 3x² – 4y² + y = 9 at (2, 1)

\[A.\ \frac{-12}{7}\]

\[B.\ \frac{12}{7}\]

\[C.\ \frac{-12}{8}\]

\[D.\ \frac{12}{8}\]

\[36.\ IF\ f\left(x\right)=\frac{1}{x^2},\ then\ f"\left(x\right)?\]

\[A.\ \frac{6}{x^4}\]

\[B.\ \frac{2}{x^3}\]

\[C.\ \frac{-6}{x^4}\]

\[D.\ \frac{-2}{x^3}\]

37. What is the area between the curve y = – x² + 4 and the x – axis? (Round your answer to nearest integer)

A. – 11

B. 10.66

C. 11

D. 12

\[38.\ IF\ \frac{dy}{dx}=3x^2y\ and\ y\left(0\right)=2,\ Find\ an\ equation\ For\ y\ in\ terms\ of\ x.\]

A. y = x3 + 2

B. y = lnx3 + 2

\[C.\ y=e^{x^3}+2\]

\[D.\ y=2e^{x^3}\]

39. If A = 3i – 4j and B = 5i + 2j, find the dot product.

A. 6

B. 7

C. 8

D. 9

40. Simplify

-7(-a³ + 5 – 2b²)

A. – 7 a³ + 5 – 2b²

B. 7a³ + 35 – 14b²

C. 7a³ – 35 + 14b²

D. 14a³b² – 35

41. Find the horizontal asymptote of the function below

\[\frac{2x+3}{x^2+1}\]

A. y = 2

B. y = 0

C. y = 5

D. No horizontal asymptote

Answer Keys

1. C
2. C
3. B
4. A
5. D
6. C
7. C
8. D
9. A
10. D
11. C
12. A
13. A
14. D
15. A
16. 4
17. D
18. A
19. A
20. B
21. B
22. C
23. B
24. A
25. D
26. C
27. B
28. A
29. B
30. B
31. C
32. A
33. C
34. D
35. B
36. A
37. C
38. D
39. B
40. C
41. B

40+ EmSAT Math Sample Questions with Answer Keys PDF

Inquiry Now for Offline or Online EmSAT Preparation