Question 1:
The figure below contains two semicircles that are tangent to each other at point B and ray DE is tangent to both semicircles at points E and F.
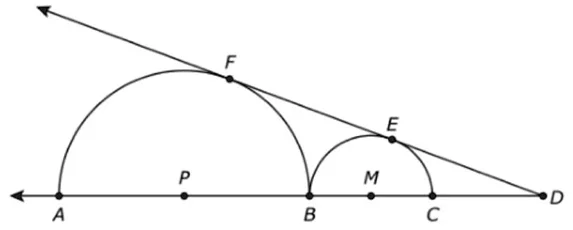
If PB = BC = 6, what does the line segment ED equals?
\[A.\ \ 6\sqrt{2}\]
\[B.\ 4\sqrt{3}\]
C. 6
D. 8
Answer Explanation
Given, PB = 6 and BC = 6.
PB = PF = 6, radius of the larger circle
BC = 6 is the diameter of the smaller circle, so radius of smaller circle is half of the diameter
\[Radius\ =\frac{Diameter}{2},\ that\ is\ BM=BC=ME=3\]
Line segment FD and ED are tangent to the circle at F and E.
\[In\ Triangle\ PFD,\ ∠F=90°\ \left(by\ radius\ \tan gent\ theorem\right)\]
\[In\ Triangle\ MED,\ ∠E=90°\ \left(by\ radius\ \tan gent\ theorem\right)\]
In Triangle PED and Triangle MED
\[∠P=∠M,\ ∠F=∠E\ and\ ∠D\ iscommonforboththetriangles.Asallthethreeanglesoftrianglesareequal,\ triangle\ PED\ andtriangle\ MED\ aresimilartriangles.\]
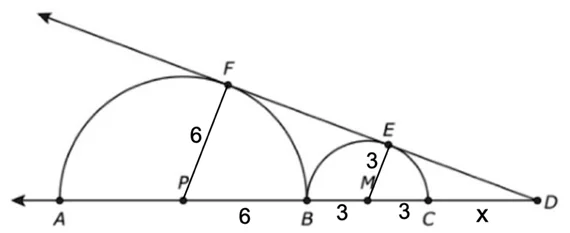
To find ED, first you need to find the length MD of triangle EMD. Let’s take length of line segment CD is equal to x and apply similarity rule.
\[\frac{PF}{ME}=\frac{PD}{MD}\]
As PF = 6 and ME = 3, Length of segment PD = 6 + 3 + 3 + x which is PD = 12 + x and length of segment MD = 3 + x
By substituting,
\[\frac{6}{3}=\frac{12+x}{3+x}\]
By cross multiplication and rearrange the expression, you will get x = 6.
Length of MD = 3 + 6, which is MD = 9.
\[In\ triangle\ MED\ ∠E=90\ and\ MD\ is\ hypotensure.\]
To find length ED, apply Pythagorean theorem
\[\left(MD\right)^2=\left(ME\right)^2+\left(ED\right)^2\ which\ is\ 9^2=3^2+\left(ED\right)^2\]
\[ED=\sqrt{9^2-3^2}\]
\[ED=6\sqrt{2}\]
Option A is the correct answer
Question 2:
A storage tank is in the shape of a cylinder with a hemisphere on the top. The highest point on the inside of the storage tank is 13 meters above the floor of the storage tank, and the diameter inside the cylinder is 8 meters.
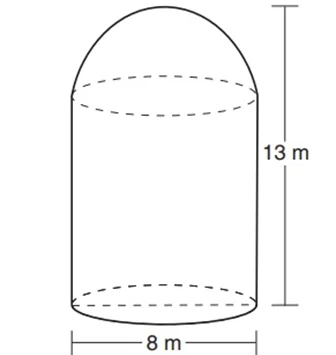
What is the volume inside the storage tank, to the nearest cubic meters?
\[Valume=\ \left(\right)m^3\]
Answer explanation
Volume of tank = Volume of cylinder + Volume of hemisphere
\[V_{\tan k=V_{cylinder}+V\ _{hemisphere}}\]
Given:
Diameter, d = 8 m so radius, r = 4 m
Height of the cylinder, h = 13 – 4 = 9 m
\[V_{cylinder=\pi r^2h}\]
\[=\pi\times4^2\times9=144\pi\]
\[V_{hemisphere}=\frac{2}{3}\pi r^3\]
\[=\frac{2}{3}\pi\times4^3=\frac{128}{3}\pi\]
\[V_{\tan k}=144\pi+\frac{128}{3}\pi=586.430\]
Round to the nearest cubic meter, V tank = 586 m3
Question 3:
A company makes cones out of solid foam. Each cone has a height of 10 cm, and its base has a diameter of 12 cm. How much foam is needed to make 45 cones?
\[Use\ \pi=3.14\ and\ round\ your\ answer\ to\ the\ nearest\ whole\ number\]
\[\left(\ \ \ \ \ \ \ \right)\ cm^3\]
Answer Explanation
Diameter, d = 12 cm. Radius, r = 6 cm.
Height, h = 10 cm
To find total amount of foam needed to make 45 cones, find the volume of a cone and multiply it by 45.
\[Volume\ of\ a\ cone,\ V=\frac{1}{3}\pi r^2h\]
\[V=\frac{1}{3}\times3.14\times6^2\times10\]
\[V=376.8\ cm^3\]
For 45 cones, total foam needed is 45×376.8 cm3
Total foam = 16,956 cm3
Question 4:
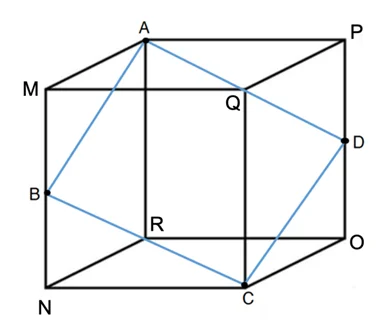
In the figure shown below, square ABCD is inscribed in a cube. Length of the side AP is 6 m. If B and D are midpoint of MN and OP. Find area and perimeter of ABCD.
Area = ( )
Perimeter = ( )
Answer Explanation
Given, AP = 6 m
B and D are midpoint of MN and OP.
Length of sides of a cube are equal, so AP = PO = AM = MN = NC = CO = 6 m
To find area and perimeter of a square, find side length of AD of a square ABCD.
\[In\ Triangle\ APD,\ PD=3m,\ AP=6\ m\ and\ angle,\ ∠P=90°\]
APD is a right-angle triangle and side AD is the hypotenuse.
Apply Pythagorean rule to find length of side AD
\[AD^2=AP^2+PD^2\]
\[AD^2=6^2+3^2\]
\[AD=\sqrt{6^2+3^2}\]
\[AD=3\sqrt{5}\]
\[Area\ of\ square,\ A=side^2\ Area=\left(3\sqrt{5}\right)^2=45\]
Perimeter of square, P = 4 X side
\[P=4x3\sqrt{5}=12\sqrt{5}\]
Question 5:
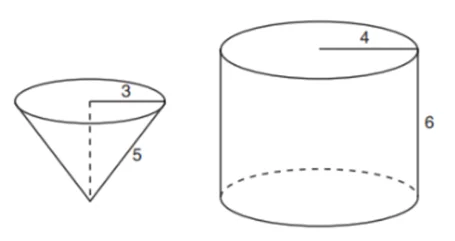
A right circular cone with a radius of 3 cm has a slant height of 5 cm.
A right cylinder with a radius of 4 cm has a height of 6 cm.
What is the number of full cones of water needed to completely fill the cylinder with this water?
Answer = ( )
Answer Explanation
Given,
Radius of cone, r = 3 cm
Slant height of cone, s = 5 cm
Height of cylinder, h = 6 cm
Radius of cylinder, r = 4 cm
To know number of cones of water needed to fill the cylinder, find volume of the cone and volume of the cylinder and then divide volume of cylinder by volume of cone.
\[Number\ of\ cones\ of\ water\ needed=\frac{volume\ of\ cylinder}{volume\ of\ cone}\]
Volume of the cone:
\[V_{cone}=\frac{1}{3}\pi r^2h\]
To find volume, find height of the cone by applying Pythagorean rule
\[5^2=h^2+3^2\]
\[h=\sqrt{5^2-3^2}which\ gives,\ h=4\ cm\]
\[Volume,\ V_{cone}=\frac{1}{3}\pi\times3^2\times4=12\ \pi\]
Find volume of cylinder:
\[V_{cylinder}=\pi r^2h\]
\[V_{cylinder}=\pi\times4^2\times6=96\ \pi\]
\[Numberofconesofwaterneeded=\frac{96\ \pi}{12\ \pi}=8\]
8 cones of water are needed to fill the cylinder
Ready to ace the EmSAT Math test? Join our online or offline classroom training today and get expert guidance to excel in your exam. Don’t miss this opportunity to boost your math skills and achieve your best score!
050 658 5644 Call / WhatsApp



